Гипо́теза Ко́ллатца (3n+1 диле́мма, сираку́зская пробле́ма) — одна из нерешённых проблем математики. Получила широкую известность благодаря простоте формулировки. Названа по имени немецкого математика Лотара Коллатца, сформулировавшего похожую задачу 1 июля 1932 года[1].
Формулировка
правитьДля объяснения сути гипотезы рассмотрим следующую последовательность чисел, называемую сираку́зской после́довательностью. Берём любое натуральное число n. Если оно чётное, то делим его на 2, а если нечётное, то умножаем на 3 и прибавляем 1 (получаем 3n + 1). Над полученным числом выполняем те же самые действия, и так далее.
Гипотеза Коллатца заключается в том, что какое бы начальное число n мы ни взяли, рано или поздно мы получим единицу[2].
Примеры
правитьНапример, для числа 3 получаем:
- 3 — нечётное, 3×3 + 1 = 10
- 10 — чётное, 10:2 = 5
- 5 — нечётное, 5×3 + 1 = 16
- 16 — чётное, 16:2 = 8
- 8 — чётное, 8:2 = 4
- 4 — чётное, 4:2 = 2
- 2 — чётное, 2:2 = 1
- 1 — нечётное.
Последовательность, начинающаяся числом 19, приходит к единице уже за двадцать шагов:
- 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, …
Для числа 27 получаем:
- 27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1
Жирным выделены нечётные числа.
Последовательность пришла к единице только через 111 шагов, достигнув в пи́ке значения 9232.
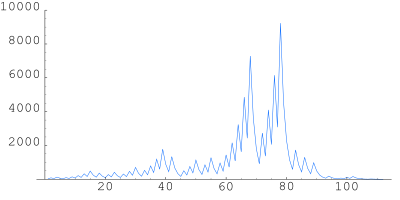
Чи́сла-гра́дины — также распространённое название для совокупности рассмотренных последовательностей. Такое название возникло из-за того, что графики последовательностей (см. иллюстрацию) похожи на траектории движения градин в атмосфере.
Последовательность первых чисел
править| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 1 | 10 | 2 | 16 | 3 | 22 | 4 | 28 | 5 | 34 | 6 | 40 | 7 | 46 | 8 | |
| 5 | 1 | 8 | 10 | 11 | 2 | 14 | 16 | 17 | 3 | 20 | 22 | 23 | 4 | ||
| 16 | 4 | 5 | 34 | 1 | 7 | 8 | 52 | 10 | 10 | 11 | 70 | 2 | |||
| 8 | 2 | 16 | 17 | 22 | 4 | 26 | 5 | 5 | 34 | 35 | 1 | ||||
| 4 | 1 | 8 | 52 | 11 | 2 | 13 | 16 | 16 | 17 | 106 | |||||
| 2 | 4 | 26 | 34 | 1 | 40 | 8 | 8 | 52 | 53 | ||||||
| 1 | 2 | 13 | 17 | 20 | 4 | 4 | 26 | 160 | |||||||
| 1 | 40 | 52 | 10 | 2 | 2 | 13 | 80 | ||||||||
| 20 | 26 | 5 | 1 | 1 | 40 | 40 | |||||||||
| 10 | 13 | 16 | 20 | 20 | |||||||||||
| 5 | 40 | 8 | 10 | 10 | |||||||||||
| 16 | 20 | 4 | 5 | 5 | |||||||||||
| 8 | 10 | 2 | 16 | 16 | |||||||||||
| 4 | 5 | 1 | 8 | 8 | |||||||||||
| 2 | 16 | 4 | 4 | ||||||||||||
| 1 | 8 | 2 | 2 | ||||||||||||
| 4 | 1 | 1 | |||||||||||||
| 2 | |||||||||||||||
| 1 |
Проект «Collatz Conjecture»
правитьВ августе 2009 года на платформе BOINC был запущен проект добровольных распределённых вычислений «Collatz Conjecture»[3], целью которого является проверка гипотезы Коллатца на больших числах. Вычислительный модуль проекта может использовать вычислительные мощности современных видеокарт.
Кроме проекта Collatz Conjecture, с августа 2017 года поиском решения этой проблемы стал также заниматься проект распределённых вычислений yoyo@home[4].
В последние годы проверены все натуральные числа до 3×1020, и каждое из них продемонстрировало соответствие гипотезе Коллатца.
Реализация на языках программирования
правитьJava:
public static ArrayList<Integer> conjectureCollatz (int n) {
//создадим коллекцию для хранения всего ряда чисел
ArrayList<Integer> arrayList = new ArrayList<>();
System.out.println("Исходное значение числа " + n);
//создадим переменную для хранения количества шагов
int stepCount = 0;
while (n != 1) {
//увеличиваем значение счетчика шагов
stepCount++;
//если число четное, то делим на 2
if (n % 2 == 0) {
n /= 2;
//если число нечетное, то умножаем на 3 и прибавляем 1
} else {
n = (n * 3) + 1;
}
//добавляем текущее число в коллекцию
arrayList.add(n);
//выводим текущее значение
System.out.println("На шаге " + stepCount + " значение n равно " + n);
}
//выводим количество шагов алгоритма
System.out.println("stepCount = " + stepCount);
//возвращаем значение коллекции
return arrayList;
}
maxnum = 0
num = int(input("Введите число: "))
while num != 1:
if num % 2 == 0:
num //= 2
else:
num = num*3 + 1
print(num)
maxnum = max(maxnum, num)
print("Пик:", maxnum)
int n;
int i = 0;
Console.WriteLine("Введите число n: ");
n = int.Parse(Console.ReadLine());
while (n != 1) {
if (n % 2 == 0) {
n /= 2;
i += 1;
}
else {
n = 3 * n + 1;
i += 1;
}
}
Console.WriteLine($"{n} {i}");
C++:
#include <iostream>
int main() {
int maxnum = 0;
int num = 0;
int count = 0;
std::cin >> num;
while (num != 1) {
if (num % 2 == 0) {
num = num / 2;
} else {
num = num * 3 + 1;
}
std::cout << num << std::endl;
maxnum = std::max(maxnum, num);
count++;
}
std::cout << "Пик: " << maxnum << std::endl;
std::cout << "Шагов: " << count << std::endl;
}
См. также
править- Открытые математические проблемы
- FRACTRAN — эзотерический язык программирования, полный по Тьюрингу, со схожими инструкциями. Показывает, что подобные задачи не имеют алгоритмического решения.
Примечания
править- ↑ Уинклер П. Математические головоломки. Коллекция гурмана. — МЦНМО, 2024. — 176 с. — ISBN 978-5-4439-1819-8.
- ↑ Стюарт, 2015, с. 405.
- ↑ Официальный сайт проекта «Collatz Conjecture» Архивная копия от 4 декабря 2017 на Wayback Machine.
- ↑ Сайт проекта «yoyo@home» Архивная копия от 22 сентября 2017 на Wayback Machine.
Литература
править- Хэйес, Брайан. Взлёты и падения чисел-градин // В мире науки (Scientific American, издание на русском языке). — 1984. — № 3. — С. 102—107.
- Стюарт, Иэн. Величайшие математические задачи. — М.: Альпина нон-фикшн, 2015. — 460 с. — ISBN 978-5-91671-318-3.
- Jeff Lagarias. The 3x+1 problem and its generalizations (англ.) // American Mathematical Monthly. — 1985. — Vol. 92. — P. 3—23.
Ссылки
править- последовательность A014682 в OEIS.
- Самая простая нерешённая задача — гипотеза Коллатца (YOUTUBE) (Видео). www.youtube.com. Дата обращения: 2 ноября 2022. Архивировано 2 ноября 2022 года.
- Das Collatz-Problem интерактивные скрипты Юргена Денкерта для решения (3n+1)- и (3n−1)-задач, создаёт последовательность для чисел любой длины, также выдаёт статистику последовательности.
- Collatz Conjecture Архивная копия от 4 декабря 2017 на Wayback Machine — проект распределённых вычислений на платформе BOINC по проверке гипотезы Коллатца на больших числах.
- On the 3x + 1 problem Архивная копия от 14 декабря 2013 на Wayback Machine — проект распределённых вычислений, основанный Эриком Рузендалем (Eric Roosendaal), по проверке гипотезы Коллатца на больших числах.
- Аналитический подход к проблеме Коллатца Архивная копия от 20 марта 2013 на Wayback Machine. (англ.)
- Реализация сиракузской последовательности на разных языках программирования Архивная копия от 4 апреля 2018 на Wayback Machine (на сайте Rosetta Code[англ.]).
- Collatz conjecture A.A Durmagambetov, A. A Durmagambetova. https://www.researchgate.net/publication/359521315_Collatz_conjecture
В другом языковом разделе есть более полная статья Collatz conjecture (англ.). |