Центральная предельная теорема
Центра́льные преде́льные теоре́мы (ЦПТ) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.

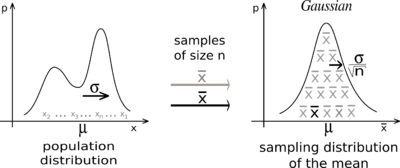
Так как многие случайные величины в приложениях формируются под влиянием нескольких слабо зависимых случайных факторов, их распределение считают нормальным. При этом должно соблюдаться условие, что ни один из факторов не является доминирующим. Центральные предельные теоремы в этих случаях обосновывают применение нормального распределения.
Классическая ЦПТ
правитьПусть есть последовательность независимых одинаково распределённых случайных величин, имеющих конечные математическое ожидание и дисперсию . Пусть также
- .
Тогда
- по распределению при ,
где — нормальное распределение с нулевым математическим ожиданием и стандартным отклонением, равным единице. Определяя выборочное среднее первых величин как
- ,
можно переписать результат центральной предельной теоремы в следующем виде (ЦПТ в форме Леви):
- по распределению при .
Скорость сходимости можно оценить с помощью неравенства Берри — Эссеена.
Замечания
править- Неформально говоря, классическая центральная предельная теорема утверждает, что сумма независимых одинаково распределённых случайных величин имеет распределение, близкое к . Эквивалентно, имеет распределение близкое к .
- Так как функция распределения стандартного нормального распределения непрерывна, сходимость к этому распределению эквивалентна поточечной сходимости функций распределения к функции распределения стандартного нормального распределения. Положив , получаем , где — функция распределения стандартного нормального распределения.
- Центральная предельная теорема в классической формулировке доказывается методом характеристических функций (теорема Леви о непрерывности).
- Вообще говоря, из сходимости функций распределения не вытекает сходимость плотностей. Тем не менее в данном классическом случае это имеет место.
Локальная ЦПТ
правитьВ предположениях классической формулировки, допустим в дополнение, что распределение случайных величин абсолютно непрерывно, то есть оно имеет плотность. Тогда распределение также абсолютно непрерывно, и более того,
- при ,
где — плотность случайной величины , а в правой части стоит плотность стандартного нормального распределения.
Обобщения
правитьРезультат классической центральной предельной теоремы справедлив для ситуаций гораздо более общих, чем полная независимость и одинаковая распределённость.
ЦПТ Линдеберга
править[2]Пусть независимые случайные величины определены на одном и том же вероятностном пространстве и имеют конечные математические ожидания и дисперсии: .
Пусть .
Тогда .
И пусть выполняется условие Линдеберга:
Тогда
- по распределению при .
Пусть выполнены базовые предположения ЦПТ Линдеберга. Пусть случайные величины имеют конечный третий момент. Тогда определена последовательность
- .
Если предел
- (условие Ляпунова),
то
- по распределению при .
ЦПТ для мартингалов
правитьПусть процесс является мартингалом с ограниченными приращениями. В частности, допустим, что
и приращения равномерно ограничены, то есть
Введём случайные процессы и следующим образом:
и
- .
Тогда
- по распределению при .
ЦПТ для случайных векторов
правитьПусть последовательность независимых и одинаково распределённых случайных векторов, каждый из которых имеет среднее и невырожденную матрицу ковариаций . Обозначим через вектор частичных сумм. Тогда при имеет место слабая сходимость распределений векторов
, где имеет распределение .
См. также
правитьПримечания
править- ↑ Rouaud, Mathieu. Probability, Statistics and Estimation (неопр.). — 2013. — С. 10. Архивировано 3 апреля 2017 года.
- ↑ Шуленин В. П. Математическая статистика. Ч. 3. Робастная статистика: учебник. — Томск: Издательство НТЛ, 2012. — С. 474. — 520 с. — ISBN 978-5-89503-508-5. Архивировано 20 сентября 2018 года.
Ссылки
правитьВ статье не хватает ссылок на источники (см. рекомендации по поиску). |
В другом языковом разделе есть более полная статья Central limit theorem (англ.). |