Файл:Thiel-Sen estimator.svg
Размер этого PNG-превью для исходного SVG-файла: 572 × 599 пкс. Другие разрешения: 229 × 240 пкс | 458 × 480 пкс | 733 × 768 пкс | 978 × 1024 пкс | 1955 × 2048 пкс | 2936 × 3075 пкс.
Исходный файл (SVG-файл, номинально 2936 × 3075 пкс, размер файла: 37 КБ)
История файла
Нажмите на дату/время, чтобы посмотреть файл, который был загружен в тот момент.
| Дата/время | Миниатюра | Размеры | Участник | Примечание | |
|---|---|---|---|---|---|
| текущий | 18:59, 3 ноября 2011 |  | 2936 × 3075 (37 КБ) | David Eppstein | Darker green, thicker lines |
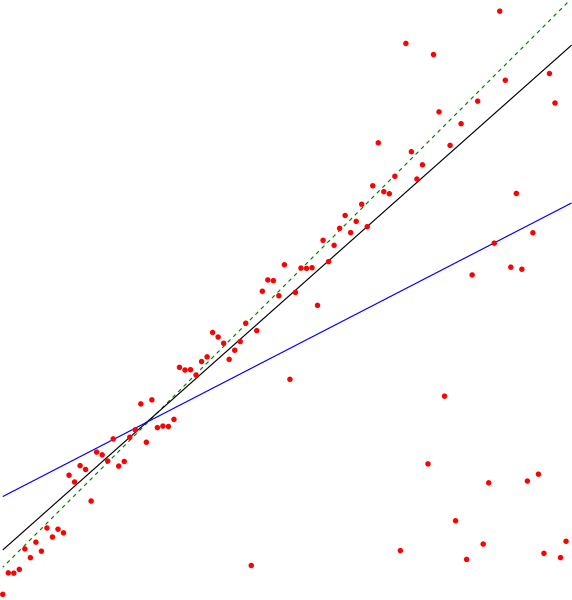
| 23:40, 3 июля 2011 |  | 2936 × 3075 (37 КБ) | David Eppstein | {{Information |Description ={{en|1=The en:Theil–Sen estimator (black line) of a set of sample points, compared to the simple linear regression line (blue). The points were generated by adding a small amount of jitter to points on the green dashe |
Использование файла
Следующие 2 страницы используют этот файл:
Глобальное использование файла
Данный файл используется в следующих вики:
- Использование в ar.wiki.x.io
- Использование в el.wiktionary.org
- Использование в en.wiki.x.io
- Использование в es.wiki.x.io
- Использование в fa.wiki.x.io
- Использование в hy.wiki.x.io
- Использование в ko.wiki.x.io
- Использование в zh.wiki.x.io