Эту страницу предлагается переименовать в «Множество всех подмножеств». |
Множество всех подмножеств (булеан, показательное множество) — множество, состоящее из всех подмножеств данного множества (включая пустое множество и само множество ); обозначается или (так как оно соответствует множеству отображений из в ).
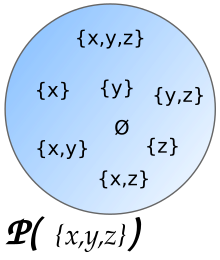
Если два множества равномощны, то равномощны и соответствующие множества всех подмножеств. Обратное утверждение (то есть инъективность операции для кардиналов) является независимым от ZFC.
В категории множеств можно снабдить функцию структурой ковариантного или контравариантного функтора следующим образом:
Мощность конечного множества подмножеств
правитьСправедливо следующее утверждение: число подмножеств конечного множества, состоящего из элементов, равно . Результат доказывается методом математической индукции. База индукции: у пустого множества ( ) только одно подмножество — оно само, и . Шаг индукции: пусть утверждение установлено для множеств мощности . Рассмотрим произвольное множество с кардинальным числом . Если зафиксировать некоторый элемент , подмножества множества разделяются на два семейства:
- , элементы которого содержат ,
- , элементы которого не содержат , то есть являются подмножествами множества .
Подмножеств второго типа по предположению индукции , однако подмножеств первого типа ровно столько же. С одной стороны, из каждого подмножества второго типа можно получить подмножество первого типа добавлением элемента . С другой стороны, из каждого подмножества первого типа можно получить подмножество второго типа удалением элемента . Следовательно,
- и .
По индукционному предположению и , то есть:
- .
См. также
правитьПримечания
правитьЛитература
править- Брудно А. Л. Теория функций действительного переменного. — М.: Наука, 1971. — 119 с.
В статье не хватает ссылок на источники (см. рекомендации по поиску). |










