Полигональная сетка (жарг. меш от англ. polygon mesh) — это совокупность вершин, рёбер и граней, которые определяют форму многогранного объекта в трёхмерной компьютерной графике и объёмном моделировании. Гранями обычно являются треугольники, четырёхугольники или другие простые выпуклые многоугольники (полигоны), так как это упрощает рендеринг, но сетки могут также состоять и из наиболее общих вогнутых многоугольников[прояснить], или многоугольников с отверстиями.
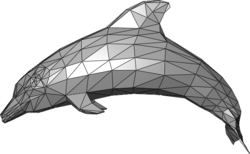
Учение о полигональных сетках — это большой подраздел компьютерной графики и геометрического моделирования. Множество операций, проводимых над сетками, может включать булеву алгебру, сглаживание, упрощение и многие другие. Разные представления полигональных сеток используются для разных целей и приложений. Для передачи полигональных сеток по сети используются сетевые представления, такие как «потоковые» и «прогрессивные» сетки. Объёмные сетки отличаются от полигональных тем, что они явно представляют и поверхность и объём структуры, тогда как полигональные сетки явно представляют лишь поверхность, а не объём. Так как полигональные сетки широко используются в компьютерной графике, для них разработаны алгоритмы трассировки лучей, обнаружения столкновений и динамики твёрдых тел.
Математический эквивалент полигональных сеток — неструктурированные сетки — изучаются методами комбинаторной геометрии.
Элементы моделирования сетки
правитьОбъекты, созданные с помощью полигональных сеток, должны хранить разные типы элементов, такие как вершины, рёбра, грани, полигоны и поверхности. Во многих случаях хранятся лишь вершины, рёбра и либо грани, либо полигоны. Рендерер может поддерживать лишь трёхсторонние грани, так что полигоны должны быть построены из их множества, как показано на рис. 1. Однако многие рендереры поддерживают полигоны с четырьмя и более сторонами, или умеют триангулировать полигоны в треугольники на лету, делая необязательным хранение сетки в триангулированной форме. Также в некоторых случаях, таких как моделирование головы, желательно уметь создавать и трёх- и четырёхсторонние полигоны.
Вершина — это позиция вместе с другой информацией, такой как цвет, вектор нормали и координаты текстуры. Ребро — это соединение между двумя вершинами. Грань — это замкнутое множество рёбер, в котором треугольная грань имеет три ребра, а четырёхугольная — четыре. Полигон — это набор компланарных (лежащих в одной плоскости) граней. В системах, которые поддерживают многосторонние грани, полигоны и грани равнозначны. Однако, большинство аппаратного обеспечения для рендеринга поддерживает лишь грани с тремя или четырьмя сторонам, так что полигоны представлены как множество граней. Математически, полигональная сетка может быть представлена в виде неструктурированной сетки, или неориентированного графа, с добавлением свойств геометрии, формы и топологии.
Поверхности, чаще называемые группами сглаживания, полезны, но не обязательны для группирования гладких областей. Представьте себе цилиндр с крышками, такой как жестяная банка. Для гладкого затенения сторон, все нормали должны указывать горизонтально от центра, тогда как нормали крышек должны указывать в +/-(0,0,1) направлениях. Если рендерить как единую, затенённую по Фонгу поверхность, вершины складок имели бы неправильные нормали. Поэтому, нужен способ определения где прекращать сглаживание для того, чтобы группировать гладкие части сетки, также, как полигоны группируют трёхсторонние грани. Как альтернатива предоставлению поверхностей/групп сглаживания, сетка может содержать другую информацию для расчёта тех же данных, такая как разделяющий угол (полигоны с нормалями выше этого предела либо автоматически рассматриваются как отдельные группы сглаживания, либо по отношению к ребру между ними применяется какая-либо техника, как например разделение или скашивание). Также, полигональные сетки с очень высоким разрешением менее подвержены проблемам, для решения которых требуются группы сглаживания, так как их полигоны настолько малы, что нужда в них пропадает. Кроме того, альтернатива существует в возможности просто отсоединения самих поверхностей от оставшейся части сетки. Рендереры не пытаются сглаживать рёбра между несмежными полигонами.
Формат полигональной сетки может определять и другие полезные данные. Могут быть определены группы, которые задают отдельные элементы сетки и полезны для установления отдельных подобъектов для скелетной анимации или отдельных субъектов нескелетной анимации. Обычно определяются материалы, позволяя разным частям сетки использовать разные шейдеры при рендере. Большинство форматов сетки также предполагают UV координаты, которые являются отдельным двухмерным представлением полигональной сетки, «развёрнутым» чтобы показать какая часть двумерной текстуры применяется к разным полигонам сетки.
Представления
правитьПолигональные сетки могут быть представлены множеством способов, используя разные способы хранения вершин, рёбер и граней. В них входят:
- Список граней: описание граней происходит с помощью указателей в список вершин.
- «Крылатое» представление: в нём каждая точка ребра указывает на две вершины, две грани и четыре (по часовой стрелке и против часовой) ребра, которые её касаются. Крылатое представление позволяет обойти поверхность за постоянное время, но у него бо́льшие требования по памяти хранения.
- Полурёберные сетки: способ похож на «крылатое» представление, за исключением того, что используется информация обхода лишь половины грани.
- Четырёхрёберные сетки[неизвестный термин], которые хранят рёбра, полурёбра и вершины без какого-либо указания полигонов. Полигоны прямо не выражены в представлении, и могут быть найдены обходом структуры. Требования по памяти аналогичны полурёберным сеткам.
- Таблица углов, которые хранят вершины в предопределённой таблице, такой что обход таблицы неявно задаёт полигоны. В сущности, это «веер треугольников», используемый в аппаратном рендеринге. Представление более компактное и более производительное для нахождения полигонов, но операции по их изменению медленны. Более того, таблицы углов не представляют сетки полностью. Для представления большинства сеток нужно несколько таблиц углов (вееров треугольников).
- Вершинное представление: представлены лишь вершины, указывающие на другие вершины. Информация о гранях и рёбрах выражена неявно в этом представлении. Однако, простота представления позволяет проводить над сеткой множество эффективных операций.
Каждое из представлений имеет свои преимущества и недостатки.[1]
Выбор структуры данных определяется применением, необходимой производительностью, размером данных, операциями, которые будут выполняться. К примеру, легче иметь дело с треугольниками, чем с многоугольниками общего вида, особенно в вычислительной геометрии. Для определённых операций необходимо иметь быстрый доступ к топологической информации, такой как рёбра или соседние грани; для этого требуются более сложные структуры, такие как «крылатое» представление. Для аппаратного рендеринга нужны компактные, простые структуры; поэтому в API низкого уровня, такие как DirectX и OpenGL обычно включена таблица углов (веер треугольников).
Вершинное представление
правитьВершинное представление описывает объект как множество вершин, соединённых с другими вершинами. Это простейшее представление, но оно не широко используемое, так как информация о гранях и рёбрах не выражена явно. Поэтому нужно обойти все данные чтобы сгенерировать список граней для рендеринга. Кроме того, нелегко выполняются операции на рёбрах и гранях.
Однако, сетки ВП извлекают выгоду из малого использования памяти и эффективной трансформации. Рисунок 2 показывает пример параллелепипеда изображённый с использованием ВП сетки. Каждая вершина индексирует её соседние вершины. Заметьте, что последние две вершины, 8 и 9 сверху и снизу параллелепипеда, имеют четыре связанных вершины, а не пять. Главная система должна справляться с произвольным числом вершин связанных с любой данной вершиной.
Для более детального описания сеток ВП см. Smith (2006)(англ.).[1]
Список граней
правитьСетка с использованием списка граней представляет объект как множество граней и множество вершин. Это самое широко используемое представление, будучи входными данными типично принимаемыми современным графическим оборудованием.
Список граней лучше для моделирования, чем вершинное представление тем, что он позволяет явный поиск вершин грани, и граней окружающих вершину. Рисунок 3 показывает пример параллелепипеда в виде сетки с использованием списка граней. Вершина v5 подсвечена, чтобы показать грани, которые её окружают. Заметьте, что в этом примере у каждой грани обязательно 3 вершины. Однако это не означает что у каждой вершины одно и то же количество окружающих граней.
Для рендеринга грань обычно посылается в графический процессор как множество индексов вершин, и вершины посылаются как позиция/цвет/структуры нормалей (на рисунке дана лишь позиция). Поэтому изменения формы, но не геометрии, могут быть динамически обновлены просто переслав данные вершины без обновления связаности граней.
Моделирование требует лёгкого обхода всех структур. С сеткой использующей список граней очень легко найти вершины грани. Также, список вершин содержит список всех граней связанных с каждой вершиной. В отличие от вершинного представления, и грани и вершины явно представлены, так что нахождение соседних граней и вершин постоянно по времени. Однако, рёбра не заданы явно, так что поиск всё ещё нужен, чтобы найти все грани, окружающие заданную грань. Другие динамические операции, такие как разрыв или объединение грани, также сложны со списком граней.
«Крылатое» представление
правитьПредставленное Брюсом Баумгартом в 1975, «Крылатое» представление явно представляет вершины, грани и рёбра сетки. Это представление широко используется в программах для моделирования для предоставления высочайшей гибкости в динамическом изменении геометрии сетки, потому что могут быть быстро выполнены операции разрыва и объединения. Их основной недостаток — высокие требования памяти и увеличенная сложность из-за содержания множества индексов.
«Крылатое» представление решает проблему обхода от ребра к ребру и обеспечивает упорядоченное множество граней вокруг ребра. Для любого заданного ребра число исходящих рёбер может быть произвольным. Чтобы упростить это, «крылатое» представление предоставляет лишь четыре, ближайшие ребра по часовой и против часовой стрелки на каждом конце ребра. Другие рёбра можно обойти постепенно. Поэтому информация о каждом ребре напоминает бабочку, поэтому представление называется «крылатым». Рисунок 4 показывает пример параллелепипеда в «крылатом» представлении. Полные данные по ребру состоят из двух вершин (конечные точки), двух граней (по каждую сторону), и четыре ребра(«крылья» ребра).
Рендеринг «крылатого» представления графическим оборудованием требует генерирования списка индексов граней. Обычно это делается только когда изменяется геометрия. «Крылатое» представление идеально подходит для динамической геометрии, такой как подразделение поверхностей и интерактивное моделирование, так как изменения сетки могут происходить локально. Обход вокруг сетки, что может пригодиться для обнаружения столкновений, может быть эффективно выполнено.
См. Baumgart (1975) для подробностей (англ.)[2]
Сводка представлений сеток
править| Операция | Вершинное представление | Список граней | «Крылатое» представление | ||
|---|---|---|---|---|---|
| V-V | Все вершины вокруг вершины | Явно | V → f1, f2, f3, … → v1, v2, v3, … | V → e1, e2, e3, … → v1, v2, v3, … | |
| E-F | Все рёбра грани | F(a, b,c) → {a, b}, {b, c}, {a, c} | F → {a, b}, {b, c}, {a, c} | Явно | |
| V-F | Все вершины грани | F(a, b,c) → {a, b,c} | Явно | F → e1, e2, e3 → a, b, c | |
| F-V | Все грани вокруг вершины | Поиск пары | Явно | V → e1, e2, e3 → f1, f2, f3, … | |
| E-V | Все рёбра вокруг вершины | V → {v, v1}, {v, v2}, {v, v3}, … | V → f1, f2, f3, … → v1, v2, v3, … | Явно | |
| F-E | Обе грани ребра | Сравнение списков | Сравнение списков | Явно | |
| V-E | Обе вершины ребра | E(a, b) → {a, b} | E(a, b) → {a, b} | Явно | |
| Flook | Найти грань с данными вершинами | F(a, b,c) → {a, b,c} | Пересечение множеств v1,v2,v3 | Пересечение множеств v1,v2,v3 | |
| Размер памяти | V*avg(V,V) | 3F + V*avg(F,V) | 3F + 8E + V*avg(E,V) | ||
| Пример с 10 вершин, 16 граней, 24 ребра: | |||||
| 10 * 5 = 50 | 3*16 + 10*5 = 98 | 3*16 + 8*24 + 10*5 = 290 | |||
| Рисунок 5: сводка операций представлений сеток | |||||
В представленной выше таблице, явно указывает на то, что операция может быть выполнена за постоянное время, так как хранятся непосредственные данные; сравнение списков указывает на то, что для выполнения операции должно быть выполнено сравнение двух списков; и поиск пары указывает на то, что должен быть выполнен поиск двух индексов. Обозначение avg(V,V) означает среднее число вершин, соединённых с заданной вершиной; avg(E,V) означает среднее число рёбер соединённых с заданной вершиной, и avg(F,V) — среднее число граней, соединённых с заданной вершиной.
Обозначение «V → f1, f2, f3, … → v1, v2, v3, …» показывает что для выполнения операции необходим обход вокруг нескольких элементов. К примеру, чтобы получить «все вершины вокруг заданной вершины V» используя список граней, нужно сначала найти грани вокруг заданной вершины V используя список вершин. Затем, из этих граней, используя список граней, найти вершины вокруг них. Заметьте, что «крылатое» представление хранит почти всю информацию в явном виде, и другие операции всегда обходят сначала ребро, чтобы получить дополнительную информацию. Вершинное представление — единственное представление, которое в явном виде хранит соседние вершины заданной вершины.
С увеличением сложности представлений (слева направо в сводке), количество информации, хранящейся в явном виде, растёт. Это даёт более прямой, постоянный по времени, доступ к обходу и топологии различных элементов, но ценой увеличения занимаемой памяти для сохранения индексов надлежащим образом.
Как общее правило, сетки использующие список граней используются всякий раз, когда объект должен рендериться с помощью аппаратного обеспечения, которое не меняет геометрию (соединения), но может деформировать или трансформировать (позиции вершин), например в рендеринге статичных или трансформируемых объектов в реальном времени. «Крылатое» представление используется когда геометрия изменяется, например в интерактивных пакетах моделирования или для вычисления подразделённых поверхностей. Вершинное представление идеально для эффективных, комплексных изменений в геометрии или топологии, пока аппаратный рендеринг не важен.
Другие представления
правитьПотоковые сетки хранят грани упорядочено, но независимо, чтобы таким образом сетку можно было пересылать по частям. Порядок граней может быть пространственным, спектральным, или базированным на других свойствах сетки. Потоковые сетки позволяют рендерить очень большие сетки даже тогда, когда они ещё загружаются.
Прогрессивные сетки передают данные о вершинах и гранях с повышающимся уровнем детализации. В отличие от потоковых сеток, прогрессивные сетки дают общую форму целого объекта, но на низком уровне детализации. Дополнительные данные, новые рёбра и грани, прогрессивно увеличивают детализацию сетки.
Нормальные сетки передают постепенные изменения сетки как множество смещений нормалей от базовой сетки. С помощью этой техники, ряд текстур отображает желаемые нарастающие изменения. Нормальные сетки компактны, так как для выражения смещения нужно лишь одно скалярное значение. Однако, техника требует ряд сложных трансформаций чтобы создать текстуры сдвига.
Файловые форматы
правитьПолигональные сетки могут храниться во множестве файловых форматов:
- .blend (Blender)
- FBX
- 3B (3D-Coat)
- 3DS
- MS3D
- Collada
- DXF
- OBJ
- PLY
- STL
- VRML
- X3D
- C4D
- MSH (формат файлов)
- iED 3D/VR Архивная копия от 16 июля 2011 на Wayback Machine
- A3D (Alternativa3D8)
- SMD
См. также
править- Полигональное моделирование
- Каркасная модель
- Операторы Эйлера
- Контурное представление
- Симплекс
- Триангуляция (геометрия)
- Многообразие (сетка может быть многообразной или немногообразной)
Примечания
править- ↑ 1 2 Colin Smith, On Vertex-Vertex Meshes and Their Use in Geometric and Biological Modeling, http://algorithmicbotany.org/papers/smithco.dis2006.pdf Архивная копия от 19 ноября 2008 на Wayback Machine
- ↑ Bruce Baumgart, Winged-Edge Polyhedron Representation for Computer Vision. National Computer Conference, May 1975. Архивированная копия. Дата обращения: 26 сентября 2005. Архивировано 29 августа 2005 года.