Экспоненциа́льное (или показа́тельное[1]) распределе́ние — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
| Показательное распределение | |
|---|---|
 Плотность вероятности Плотность вероятности | |
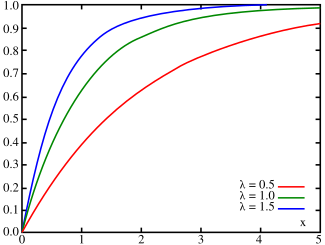 Функция распределения Функция распределения | |
| Обозначение | |
| Параметры | — интенсивность или обратный коэффициент масштаба |
| Носитель | |
| Плотность вероятности | |
| Функция распределения | |
| Математическое ожидание | |
| Медиана | |
| Мода | |
| Дисперсия | |
| Коэффициент асимметрии | |
| Коэффициент эксцесса | |
| Дифференциальная энтропия | |
| Производящая функция моментов | |
| Характеристическая функция | |
Определение
правитьСлучайная величина имеет экспоненциальное распределение с параметром , если её плотность вероятности имеет вид:
- .
Пример. Пусть есть магазин, в который время от времени заходят покупатели. При определённых допущениях время между появлениями двух последовательных покупателей будет случайной величиной с экспоненциальным распределением. Среднее время ожидания нового покупателя (см. ниже) равно . Сам параметр тогда может быть интерпретирован как среднее число новых покупателей за единицу времени.
В этой статье для определённости будем предполагать, что плотность экспоненциальной случайной величины задана первым уравнением, и будем писать: .
Функция распределения
правитьИнтегрируя плотность, получаем функцию экспоненциального распределения:
Моменты
правитьНесложным интегрированием находим, что производящая функция моментов для экспоненциального распределения имеет вид:
- ,
откуда получаем все моменты:
- .
В частности,
- ,
- ,
- .
Независимость событий
правитьПусть . Тогда .
Пример. Пусть автобусы приходят на остановку случайно, но с некоторой фиксированной средней интенсивностью. Тогда количество времени, уже затраченное пассажиром на ожидание автобуса, не влияет на время, которое ему ещё придётся прождать.
Связь с другими распределениями
править- Экспоненциальное распределение является распределением Пирсона типа X[2].
- Минимум независимых экспоненциальных случайных величин также экспоненциальная случайная величина. Пусть независимые случайные величины, и . Тогда[3]:
- Экспоненциальное распределение является частным случаем гамма-распределения:
- Сумма независимых одинаково распределённых экспоненциальных случайных величин имеет гамма-распределение. Пусть независимые случайные величины, и . Тогда:
- Экспоненциальное распределение может быть получено из непрерывного равномерного распределения методом обратного преобразования. Пусть . Тогда:
- Экспоненциальное распределение с параметром — это частный случай распределения хи-квадрат:
- Экспоненциальное распределение является частным случаем распределения Вейбулла.
- Пусть независимые случайные величины, и и . Тогда:
Примечания
править- ↑ Андрей Рукосуев, Виктор Башлыков, Константин Балдин. Основы теории вероятностей и математической статистики. Учебник. — Litres, 2016-03-26. — С. 80. — 489 с. — ISBN 9785457365889.
- ↑ Королюк, 1985, с. 135.
- ↑ Виктор Каштанов, Алексей Медведев. Теория надежности сложных систем. — 2018. — С. 498. — 608 с.
Литература
править- Королюк В. С., Портенко Н. И.,Скороход А. В., Турбин А. Ф. Справочник по теории вероятностей и математической статистике. — М.: Наука, 1985. — 640 с.
Для улучшения этой статьи желательно:
|













