Щели (или люки) Кирквуда — определённые зазоры в поясе астероидов, связанные с их орбитальным резонансном с Юпитера. В этих зазорах астероиды практически отсутствуют[1]. Астероиды не могут длительное время существовать на таких орбитах, так как из-за гравитационного влияния Юпитера эти орбиты становятся нестабильными. В результате некоторые области пояса астероидов почти не заполнены — это так называемые щели или люки Кирквуда. При этом некоторые астероиды движутся в резонансе с Юпитером, сохраняя свои орбитальные периоды. Простейшим случаем такого резонанса с соотношением периодов 1:1 и являются «троянцы».
Существование щелей было предсказано Даниэлем Кирквудом ещё в 1857 году, когда было открыто всего около 50 астероидов, что было слишком мало, чтобы подтвердить его теорию, но сейчас, когда количество открытых астероидов превысило 300 000, его правота уже не вызывает сомнений.
Орбиты астероидов
правитьЭти зазоры обнаружил американский астроном Дэниел Кирквуд в 1866 году[2]. Кирквуд установил, что астероиды избегают тех периодов, которые находятся в простом целочисленном соотношении[3] с периодом обращения Юпитера вокруг Солнца, например, 2:1, 3:1, 5:2 и т. п. Под действием гравитационного влияния Юпитера астероиды изменяют орбиту и выбрасываются из этой области пространства[4].
Так, например, есть очень мало астероидов с большой полуосью 2,5 а. е. и периодом 3,95 года, у них на три оборота вокруг Солнца приходится один оборот Юпитера. Соответственно резонанс с Юпитером будет составлять 3:1. Такой астероид будет сближаться с Юпитером на минимально возможное расстояние гораздо чаще, чем другие астероиды, находящиеся на обычных не резонансных орбитах, а именно через каждые 3 оборота. Вследствие этого, он будет регулярно испытывать на себе сильное гравитационное воздействие этой планеты, из-за чего эксцентриситет орбиты резонансных астероидов под действием гравитации планеты-гиганта будет постепенно возрастать, причём гораздо быстрее, чем у других астероидов, в результате чего астероид в конце концов выбрасывается с такой орбиты и переходит на более стабильную[5]. Этот процесс может протекать заметно интенсивнее в моменты противостояний Юпитера и Сатурна[6].
Более слабые резонансы, при которых сближения происходят менее часто, приводят к постепенному уменьшению количества астероидов, начиная с наиболее мелких. Максимальные же концентрации астероидов (пик на гистограмме) зачастую соответствуют орбитам, на которых обращаются некоторые крупные астероидные семейства.
Распределение Кирквуда представляет собой наиболее наглядный случай орбитального резонанса, аналогичный делению Кассини в кольцевой системе Сатурна.
Совсем недавно было обнаружено сравнительно небольшое число астероидов с высоким эксцентриситетом, орбиты которых лежат в области Кирквуда. Примерами таких астероидов являются семейство Алинды и семейство Гриква. Орбиты этих астероидов медленно, но неумолимо увеличивают свой эксцентриситет из-за слишком частых сближений с Юпитером, и в конечном итоге через несколько десятков миллионов лет астероиды будут выброшены гравитацией планеты-гиганта за пределы этой области.
Резонансы
правитьВ соответствии с третьим законом Кеплера можно рассчитать резонансы между некоторыми орбитами астероидов и Юпитером[7].
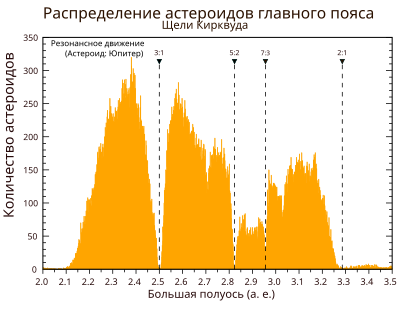
Проведя соответствующие расчёты, можно установить наиболее известные щели Кирквуда (см. диаграмму), расположенные на следующих средних орбитальных радиусах:
- 2,06 а. е. (резонанс 4:1)
- 2,5 а. е. (резонанс 3:1), орбита астероидов семейства Алинды
- 2,82 а. е. (резонанс 5:2)
- 2,95 а. е. (резонанс 7:3)
- 3,27 а. е. (резонанс 2:1), орбита астероидов семейства Гриква
Более слабые резонансные орбиты, которые тоже можно найти на карте:
- 1,9 а. е. (резонанс 9:2)
- 2,25 а. е. (резонанс 7:2)
- 2,33 а. е. (резонанс 10:3)
- 2,71 а. е. (резонанс 8:3)
- 3,03 а. е. (резонанс 9:4)
- 3,075 а. е. (резонанс 11:5)
- 3,47 а. е. (резонанс 11:6)
- 3,7 а. е. (резонанс 5:3)
См. также
править- Орбитальный резонанс
- Щель Кассини — промежутки между внешними кольцами Сатурна той же природы, что щели Кирквуда.
- Семейство астероидов
Примечания
править- ↑ Пояс астероидов между Марсом и Юпитером. Дата обращения: 23 апреля 2017. Архивировано 24 апреля 2017 года.
- ↑ Coleman, Helen Turnbull Waite. Banners in the Wilderness: The Early Years of Washington and Jefferson College (англ.). — University of Pittsburgh Press (англ.), 1956. — P. 158.
- ↑ Где делимое и делитель — «не очень большие» числа (до 10)
- ↑ Люки Кирквуда. Дата обращения: 23 апреля 2017. Архивировано 24 апреля 2017 года.
- ↑ Moons, Michèle; Morbidelli, Alessandro. Secular resonances inside mean-motion commensurabilities: the 4/1, 3/1, 5/2 and 7/3 cases (англ.) // Icarus : journal. — Elsevier, 1995. — Vol. 114, no. 1. — P. 33—50. — doi:10.1006/icar.1995.1041. — .
- ↑ Moons, Michèle; Morbidelli, Alessandro; Migliorini, Fabio. Dynamical Structure of the 2/1 Commensurability with Jupiter and the Origin of the Resonant Asteroids (англ.) // Icarus : journal. — Elsevier, 1998. — Vol. 135, no. 2. — P. 458—468. — doi:10.1006/icar.1998.5963. — .
- ↑ A record of planet migration in the main asteroid belt. Nature. doi:10.1038/nature07778. Дата обращения: 13 декабря 2016. Архивировано 21 декабря 2016 года.