Кукушкино хеширование

Кукушкино хеширование — алгоритм разрешения коллизий значений хеш-функций в таблице с постоянным временем выборки в худшем случае.

Пример кукушкиного хеширования. Стрелки показывают альтернативное положение ключа. Новое значение, которое вставляется в ячейку A, выталкивая A в альтернативную ячейку, занимаемую ключом B, значение B переносится в альтернативное место, которое в настоящее время не занято. Вставка нового значения в ячейку H завершается неудачей — H входит в цикл (вместе с W), так что только что вставленный элемент должен быть вытолкнут.

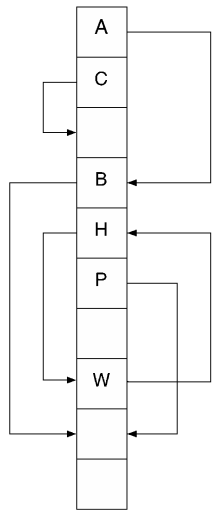
Предложено в 2001 году. Название отсылает к поведению некоторых видов кукушек, когда птенец выталкивает из гнезда яйца или других птенцов; аналогичным образом в алгоритме предусматривается возможность выталкивания старого ключа при вставке нового.

Операции

Кукушкино хеширование является видом открытой адресации, в которой каждая непустая ячейка хеш-таблицы содержит ключ или пару «ключ — значение». Хеш-функция используется для определения места для каждого ключа, и его присутствие в таблице (или значение, ассоциированное с ним) может быть найдено путём проверки этой ячейки в таблице. Однако открытая адресация страдает от коллизий, которые случаются, когда более одного ключа попадают в одну ячейку. Основная идея кукушкиного хеширования заключается в разрешении коллизий путём использования двух хеш-функций вместо одной. Это обеспечивает два возможных положения в хеш-таблице для каждого ключа. В одном из обычных вариантов алгоритма хеш-таблица разбивается на две меньшие таблицы меньшего размера и каждая хеш-функция даёт индекс в одну из этих двух таблиц. Можно обеспечить также для обеих хеш-функций индексирование внутри одной таблицы.

Выборка требует просмотра всего двух мест в хеш-таблице, что требует постоянного времени в худшем случае (см. «O» большое и «o» малое). Это контрастирует с многими другими алгоритмами хеш-таблиц, которые не обеспечивают постоянное время выборки в худшем случае. Удаление также может быть осуществлено очищением ячейки, содержащей ключ за постоянное время в худшем случае, что осуществляется проще, чем в других схемах, таких как линейное зондирование.

Когда вставляется новый ключ и одна из двух ячеек пуста, ключ может быть помещён в эту ячейку. В случае же, когда обе ячейки заняты, необходимо переместить другие ключи в другие места (или, наоборот, на их прежние места), чтобы освободить место для нового ключа. Используется жадный алгоритм — ключ помещается в одну из возможных позиций, «выталкивая» любой ключ, который был в этой позиции. Вытолкнутый ключ затем помещается в его альтернативную позицию, снова выталкивая любой ключ, который мог там оказаться. Процесс продолжается, пока не найдётся пустая позиция. Возможен, однако, случай, когда процесс вставки заканчивается неудачей, попадая в бесконечный цикл или когда образуется слишком длинная цепочка (длиннее, чем заранее заданный порог, зависящий логарифмически от длины таблицы). В этом случае хеш-таблица перестраивается на месте с новыми хеш-функциями:

Нет необходимости размещения новой таблицы для повторного хеширования — мы можем просто просматривать таблицу для удаления и повторной вставки всех ключей, которые находятся не в той позиции, в которой должны были бы стоять.Pagh & Rodler, «Cuckoo Hashing»

Вычислительная сложность

Ожидаемое время вставки постоянно, даже если принимать во внимание возможную необходимость перестройки таблицы, пока число ключей меньше половины ёмкости хеш-таблицы, то есть коэффициент загрузки меньше 50 %.

Чтобы обеспечить это, используется теория случайных графов — можно образовать неориентированный граф, называемый «кукушкиным графом», в котором вершинами являются ячейки хеш-таблицы, а рёбра для каждого хешируемого соединяют два возможных положения (ячейки хеш-таблицы). Тогда жадный алгоритм вставки множества значений в кукушкину хеш-таблицу успешно завершается тогда и только тогда, когда кукушкин граф для этого множества значений является псевдолесом, графом максимум с одним циклом в каждой компоненте связности. Любой порождённый вершинами подграф с числом рёбер, большим числа вершин, соответствует множеству ключей, для которых число слотов в хеш-таблице недостаточно. Если хеш-функция выбирается случайно, кукушкин граф будет случайным графом в модели Эрдёша – Реньи. С высокой степенью вероятности для случайного графа, в котором отношение числа рёбер к числу вершин ограничено сверху 1/2, граф является псевдолесом и алгоритм кукушкиного хеширования располагает успешно все ключи. Более того, та же теория доказывает, что ожидаемый размер компонент связности кукушкиного графа мал, что обеспечивает постоянное ожидаемое время вставки.

Пример

Если даны следующие две хеш-функции:

$h\left(k\right)=k\mod 11$

$h'\left(k\right)=\left\lfloor {\frac {k}{11}}\right\rfloor \mod 11$

k	h(k)	h'(k)
20	9	1
50	6	4
53	9	4
75	9	6
100	1	9
67	1	6
105	6	9
3	3	0
36	3	3
39	6	3

Столбцы в следующих двух таблицах показывают состояние хеш-таблицы после вставки элементов.

1. table for h(k)
	20	50	53	75	100	67	105	3	36	39
0
1					100	67	67	67	67	100
2
3								3	36	36
4
5
6		50	50	50	50	50	105	105	105	50
7
8
9	20	20	53	75	75	75	53	53	53	75
10

2. table for h'(k)
	20	50	53	75	100	67	105	3	36	39
0									3	3
1			20	20	20	20	20	20	20	20
2
3										39
4				53	53	53	50	50	50	53
5
6							75	75	75	67
7
8
9						100	100	100	100	105
10

Циклы

Если вы хотите вставить элемент 6, вы получите бесконечный цикл. В последней строке таблицы мы находим ту же начальную ситуацию, что и в начале.

$h\left(6\right)=6\mod 11=6$
$h'\left(6\right)=\left\lfloor {\frac {6}{11}}\right\rfloor \mod 11=0$

ключ	table 1		table 2
	старое значение	новое значение	старое значение	новое значение
6	50	6	53	50
53	75	53	67	75
67	100	67	105	100
105	6	105	3	6
3	36	3	39	36
39	105	39	100	105
100	67	100	75	67
75	53	75	50	53
50	39	50	36	39
36	3	36	6	3
6	50	6	53	50

Вариации

Изучались некоторые вариации кукушкиного хеширования, в основном с целью улучшить использование пространства путём увеличения коэффициента загрузки. В этих вариантах может достигаться порог загрузки больше 50 %. Некоторые из этих методов могут быть использованы для существенного уменьшения числа необходимых перестроек структуры данных.

От обобщения кукушкиного хеширования, использующего более двух хеш-функций, можно ожидать лучшего использования хеш-таблицы, жертвуя некоторой скоростью выборки и вставки. Использование трёх хеш-функций повышает коэффициент загрузки до 91 % . Другое обобщение кукушкиного хеширования, называемое блочным кукушкиным хешированием, содержит более одного ключа на ячейку. Использование двух ключей на ячейку позволяет повысить загрузку выше 80 %.

Ещё один изучавшийся вариант — кукушкино хеширование с запасом. «Запас» — это массив ключей постоянной длины, который используется для хранения ключей, которые не могут быть успешно вставлены в главную хеш-таблицу. Эта модификация уменьшает число неудач до обратно-полиномиальной функции со степенью, которая может быть произвольно большой, путём увеличения размера запаса. Однако большой запас означает более медленный поиск ключа, которого нет в основной таблице, либо если он находится в запасе. Запас можно использовать в комбинации с более чем двумя хеш-функциями или с блоковым кукушкиным хешированием для получения как высокой степени загрузки, так и малого числа неудач вставки. Анализ кукушкиного хеширования с запасом распространился и на практические хеш-функции, не только случайные модели хеш-функций, используемые в теоретическом анализе хеширования.

Некоторые исследователи предлагают использовать в некоторых кэшах процессора упрощенное обобщение кукушкиного хеширования, называемого несимметричным ассоциативным кэшем.

Сравнение с аналогичными структурами

Есть другие алгоритмы, которые используют несколько хеш-функций, в частности фильтр Блума — эффективная по памяти структура данных для нечётких множеств. Альтернативная структура данных для задач с теми же нечёткими множествами, основанная на кукушкином хешировании, называемая кукушкиным фильтром, использует даже меньшую память и (в отличие от классических фильтров Блума) позволяет удаление элемента, не только вставку и проверку существования. Однако теоретический анализ этих методов проведён существенно слабее, чем анализ фильтров Блума.

Исследования 2006 года показали, что кукушкино хеширование существенно быстрее метода цепочек для малых хеш-таблиц, находящихся в кэше современных процессоров. В том же году разработана блочная версия кукушкиного хеширования (блок содержит более одного ключа), которая работает быстрее обычных методов для больших хеш-таблиц в случае высокого коэффициента загрузки. Скорость работы блочной версии кукушкиной хеш-таблицы исследована в 2009 году.

См. также

• Совершенная функция хеширования
• Линейное зондирование
• Двойное хеширование
• Коллизия хеш-функции
• Хеширование
• Квадратичное зондирование
• Хеширование «Классики»

Литература

• Rasmus Pagh, Flemming Friche Rodler. Cuckoo Hashing // Algorithms — ESA 2001. — 2001. — Т. 2161. — С. 121–133. — (Lecture Notes in Computer Science). — ISBN 978-3-540-42493-2. — doi:10.1007/3-540-44676-1_10.
• Reinhard Kutzelnigg. Fourth Colloquium on Mathematics and Computer Science. — 2006. — Т. AG. — С. 403–406. — (Discrete Mathematics and Theoretical Computer Science).
• M. Mitzenmacher. Proceedings of of the 17th Annual European Symposium on Algorithms (ESA). — 2009.
• Martin Dietzfelbinger, Christoph Weidling. Balanced allocation and dictionaries with tightly packed constant size bins // Theoret. Comput. Sci.. — 2007. — Т. 380, вып. 1—2. — С. 47–68. — doi:10.1016/j.tcs.2007.02.054.
• Adam Kirsch, Michael D. Mitzenmacher, Udi Wieder. More robust hashing: cuckoo hashing with a stash // SIAM J. Comput.. — 2010. — Т. 39, вып. 4. — С. 1543–1561. — doi:10.1137/080728743.
• Martin Aumüller, Martin Dietzfelbinger, Philipp Woelfel. Explicit and efficient hash families suffice for cuckoo hashing with a stash // Algorithmica. — 2014. — Т. 70, вып. 3. — С. 428–456. — doi:10.1007/s00453-013-9840-x.
• Bin Fan, Michael Kaminsky, David Andersen. Cuckoo Filter: Better Than Bloom // ;login:. — USENIX, 2013. — Т. 38, вып. 4. — С. 36–40.
• Marcin Zukowski, Sandor Heman, Peter Boncz. Architecture-Conscious Hashing. — Proceedings of the International Workshop on Data Management on New Hardware (DaMoN), 2006.
• Kenneth Ross. Efficient Hash Probes on Modern Processors. — IBM Research Report RC24100, 2006.
• Nikolas Askitis. Fast and Compact Hash Tables for Integer Keys. — Proceedings of the 32nd Australasian Computer Science Conference (ACSC 2009). — 2009. — Т. 91. — С. 113–122. — ISBN 978-1-920682-72-9.

Ссылки

• A cool and practical alternative to traditional hash tables, U. Erlingsson, M. Manasse, F. Mcsherry, 2006.
• Cuckoo Hashing for Undergraduates, 2006, R. Pagh, 2006.
• Cuckoo Hashing, Theory and Practice (Part 1, Part 2 and Part 3), Michael Mitzenmacher, 2007.
• Moni Naor, Gil Segev, Udi Wieder. International Colloquium on Automata, Languages and Programming (ICALP). — Reykjavik, Iceland, 2008.
• Algorithmic Improvements for Fast Concurrent Cuckoo Hashing, X. Li, D. Andersen, M. Kaminsky, M. Freedman. EuroSys 2014.

Примеры

• Concurrent high-performance Cuckoo hashtable written in C++
• Cuckoo hash map written in C++
• Static cuckoo hashtable generator for C/C++
• Generic Cuckoo hashmap in Java (недоступная ссылка)
• Cuckoo hash table written in Haskell
• Cuckoo hashing for Go