Инъе́кция (инъекти́вное отображе́ние) в математике — отображение множества во множество (), при котором разные элементы множества переводятся в разные элементы множества , то есть если два образа при отображении совпадают, то и прообразы совпадают: .
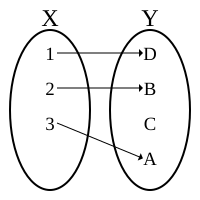
Инъекцию также называют вложением, или одно-однозначным отображением (в отличие от биекции, которая взаимно однозначна). В отличие от сюръекции, про которую говорят, что она отображает одно множество на другое, об инъекции аналогичная фраза формулируется как отображение в .
Инъекцию можно также определить как отображение, для которого существует левое обратное, то есть инъективно, если существует , при котором композиция .
Понятие инъекции (наряду с сюръекцией и биекцией) введено в трудах Бурбаки и получило широкое распространение почти во всех разделах математики.
Примеры
править- (натуральный логарифм) — инъективно и сюръективно (здесь — множество положительных чисел).
- — инъективно (здесь — множество неотрицательных чисел).
- — не является инъективным, так как .
Применение
править- Одним из прикладных примеров применения понятия инъекции является организация связи «один к одному» между сущностями в реляционной модели данных.
- Идеальная хеш-функция является инъективной.
Обобщения
править- Обобщением понятия инъекции в теории категорий является понятие мономорфизма. Во многих категориях, хотя и не во всех, эти понятия эквивалентны.
Литература
править- Н. К. Верещагин, А. Шень. Начала теории множеств // Лекции по математической логике и теории алгоритмов. (недоступная ссылка)
- Ершов Ю. Л., Палютин Е. А. Математическая логика: Учебное пособие. — 3-е, стереотип. изд. — СПб.: Лань, 2004. — 336 с.






