Число Аббе

Число́ А́ббе ($V$-число) — безразмерная величина, используемая в оптике как мера дисперсии света в прозрачных средах. Чем оно меньше, тем больше дисперсия и тем сильнее хроматическая аберрация среды.

Зависимость показателя преломления некоторых стёкол от длины волны света и расчёт числа Аббе для тяжёлого флинта SF11 при двух разных определениях трёх длин волн

Названо в честь немецкого физика Эрнста Аббе.

Определение

Число Аббе обычно определяется как:

$V={\frac {n_{\mathrm {D} }-1}{n_{\mathrm {F} }-n_{\mathrm {C} }}},$

где $n_{\mathrm {C} },\,n_{\mathrm {D} },\,n_{\mathrm {F} }$ — показатели преломления среды на длинах волн, соответствующих фраунгоферовым линиям: красная линия водорода C (656,3 нм), желтая линия натрия D (589,2 нм) и синяя линия водорода F (486,1 нм).

Такое определение даётся по умолчанию, но иногда вместо D-линии натрия используют d-линию гелия:

$V_{\mathrm {d} }={\frac {n_{\mathrm {d} }-1}{n_{\mathrm {F} }-n_{\mathrm {C} }}},$

где $n_{\mathrm {d} }$ — показатель преломления для жёлтой d-линии гелия (587,5618 нм).

В лабораторных условиях проще использовать ртутные и кадмиевые спектральные газоразрядные лампы, для которых число Аббе рассчитывается следующим образом:

$V_{\mathrm {e} }={\frac {n_{\mathrm {e} }-1}{n_{\mathrm {F'} }-n_{\mathrm {C'} }}}.$

Здесь используется e-линия ртути (546,073 нм) и линии кадмия C′ (643,8 нм), F′ (480,0 нм).

У наиболее распространённого неорганического стекла число Аббе равно 59, у полимера CR-39 — 58, у поликарбоната — 32, у воды — 54.

Иногда для характеристики дисперсии используется величина, обратная числу Аббе, называемая относительной дисперсией.

Диаграмма Аббе

Диаграмма Аббе для оптических стёкол. ЛК — лёгкие кроны; ФК — фосфатные кроны; ТФК — тяжёлые фосфатные кроны; К — кроны; БК — баритовые кроны; ТК — тяжёлые кроны; КФ — кронфлинты: БФ — баритовые флинты; ТБФ — тяжёлые баритовые флинты; ЛФ — лёгкие флинты; Ф — флинты; ТФ — тяжёлые флинты; СТФ — сверхтяжёлые флинты; СТК — сверхтяжёлые кроны.

Влияние изменения молярного состава базового стекла некоторых компонентов на число Аббе

Диаграммой Аббе называют двумерную диаграмму, на координатных осях которой откладываются числа Аббе $v_{D}$ и показатели преломления оптических стёкол $n_{D}$. На диаграмме отмечаются области, соответствующие различным типам стёкол, например, крон, флинт, боросиликатное и другие.

Приложения

Знание числа Аббе важно при конструировании оптических систем с низкой хроматической аберрацией — ахроматов. Например, ахроматическая линза, состоящая из двух тонких линз, одна из которых собирающая, а вторая — рассеивающая, имеющая отрицательное фокусное расстояние, находящихся на небольшом расстоянии друг от друга, будет иметь одинаковое фокусное расстояние для линий Фраунгофера F (синяя, 486,1327 нм) и С (красная, 656,2725 нм) если:

$V_{1}\ f_{1}+V_{2}\ f_{2}=0,$

где $V_{1},\ V_{2}$ — числа Аббе материала линз;

$f_{1},\ f_{2}$ — фокусные расстояния.

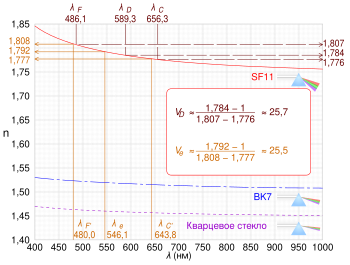
Такая система линз фокусирует синие и красные лучи с длинами волн 486 нм (F) и 656 нм (C) в одной плоскости. Лучи с другой длиной волны в такой системе не обязательно фокусируются в той же плоскости. Ошибка сведения фокусов лучей, присущая ахроматам (так называемый вторичный спектр), даёт фиолетовую кайму вокруг изображений ярких предметов. В более сложных оптических системах — апохроматах, применяются несколько линз с разными фокусными расстояниями и изготовленные из стекла с разными тщательно подобранными числами Аббе удаётся уравнять фокусные расстояния системы для лучей трёх и более длин волн. Варьируя химический состав стекла можно получить оптические стёкла с заданным числом Аббе, как показано на рисунке.

В оптических системах рассеивающие и собирающие линзы с разными показателями преломления и разными числами Аббе обычно склеивают. Склеенные объективы-ахроматы применялись в крупных телескопах создаваемых в XIX веке.

В инфракрасном и ультрафиолетовом диапазонах число Аббе, которое определено измерениями показателя преломления для длин волн в видимом диапазоне, непригодно для коррекции хроматической аберрации.

Литература

• Safa O. Kasap, Peter Capper. Springer handbook of electronic and photonic materials. — Springer, 2006. — 1406 p. — ISBN 9780387260594.
• Virendra N. Mahajan Ray geometrical optics

Ссылки

• Стекло оптическое бесцветное. Технические условия.